Answering Multi-Dimensional Range Queries under Local Differential Privacy

摘要

在LDP的保证下回答多维范围查询主要会遇到以下三个关键技术挑战：

（1）捕获属性之间的关联；

（2）处理维度多的范围查询；

（3）处理取值范围大的属性；

为了解决以上三个挑战，该文献首先提出了TDG算法（只采用二维网格）。然而这种算法丢失了单个属性的分布信息，因此为了解决该问题，进一步提出了HDG算法（一维网格与二维网格相结合），且大量的实验表明HDG算法的性能较于现有的算法有了较大的提升。

1.介绍

多维范围查询：获取同时满足多个属性的限制条件的用户频率；

现有的解决范围查询的算法大部分受限于对单个属性的一维查询，并且不能很好地拓展到处理高维范围查询。该文献首先提出了TDG算法，其主要思想为将所有可能出现的属性对构成的二维域划分为可以回答所有二维查询的二维网格，然后根据这些相关的二维查询去回答更高维度的范围查询。然后提出了一个升级版的方法HDG算法，其主要思想为组合混合维度（一维网格和二维网格）的信息去进行更好的估计。在这两个算法中，用户都被分成组，每个组向一个网格报告其信息。在满足LDP的前提下将每个网格的频率都收集完后，融合中心使用技术实现网格的非负性和一致性，并且最终采用这些网格去回答范围查询。

总的来说，该文献的贡献如下：

（1）提出了TDG算法和HDG算法用于在LDP环境下回答多维范围查询，并且提供了基于不同来源的误差分析去选择网格粒度的基本准则；

（2）开展了大量的实验通过比较不同的算法去评估算法的性能，实验结果表明HDG算法比现有的算法高出一个数量级。

2.初步——用户划分原则

用户分组在现有的LDP算法很常见。也就是说，当需要多个信息时，首先需要将所有用户进行分组，然后再从每个用户组中收集信息来获得最佳结果。

3.多维范围查询和基线算法

3.1多维范围查询

假设有d个有序属性{a₁, a₂, … , a_d}，不失一般性，假设每个属性有相同的取值范围[c] = {1, 2, … , c}，其中c是2的指数幂。用户总数量用n表示，第i个用户的隐私值是一个d维向量vi = <v¹_i, v²_i, … , v^d_i, >。正式地，一个λ维范围查询q定义如下图所示：

定义A_q代表范围查询q所涉及到的所有属性，那么q的真实结果如下图所示：

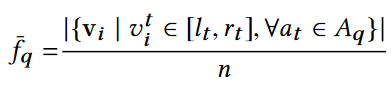
3.2基线算法

3.2.1边缘列联表发布算法

3.2.1.1全列联表法（Full Contingency Table Method，FC）

算法思想：根据所有用户在通过LDP扰动后上传的数据构建一个全列联表F，然后再通过F构建所有的边缘列联表；

算法缺点：时间复杂度和空间复杂度都随着属性数量d的增加而指数级增加，当d很大时，实际的时空开销是不可接受的。一般来说，假设Var₀表示全列联表中每个单元的方差，那么计算k-路边缘列联表的方差如下图所示：

3.2.1.2全边缘列联表法（All Marginal Method，AM）

算法思想：因为FC算法构建的k-路边缘列联表的方差与属性数量d呈指数级增长，因此考虑使用融合中心直接构建所有的k-路边缘列联表；

实现途径：第一种途径是用户将其隐私预算分成C^k_d份，然后上传C^k_d次数据，即每次上传一个k-路边缘列联表；第二种途径是将所有用户划分成C^k_d个不同的用户组，每个用户只需上传一个k-路边缘列联表（一般来说，LDP场景下划分用户比划分隐私预算能获得更好的精度，因为划分隐私意味着每个k-路边缘列联表的隐私预算更小，那么就会被注入更大的噪声）。其中，因为将用户划分为C^k_d个组会给构建k-路边缘列联表带来C^k_d倍的影响，所以第二种算法的方差为：

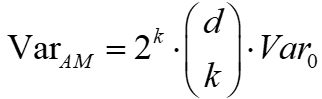
算法不足：当k很大时，AM算法的精度会受到很大的影响；该算法的另外一个局限性在于k需要事先指定，且当融合中心完成所有k-路边缘列联表的构建时，无法再获取t-路边缘列联表（t>k）。

3.2.1.3CALM

算法思想：收集低纬度的边缘列联表并据此构建一个高维列联表；

算法评价：CALM算法捕获了必要的属性之间的联系且解决了多维范围查询问题，但是没能处理取值范围大的属性。因为当属性的取值范围很大时，会在查询结果中引入大量的噪声。

3.2.2HIO

算法不足：HIO算法捕获了所有属性之间的联系，但是其他两个问题没有解决。因为HIO算法需要将用户分成(h+1)^d组，其中h=log_bc，而当属性数量d和属性取值范围c很大时，每个用户组的用户数量会很少，这样就会引入大量的噪声并进一步导致更大的误差。

3.2.2LHIO（待续）

3.2.3MSW（待续）

4.网格方法

4.1概述

为了同时解决前文提到的三个挑战，该文献首先提出了二维网格算法TDG，其主要思想为将所有属性对的二维取值范围划分成可以回答所有二维范围查询的二维网格，并结合相关的二维网格去回答高维的范围查询；但是由于只采用了二维网格，当采用TDG算法去进行一维范围查询时就需要借助均匀分布假设，而这就会引入大量的误差，为了解决这一问题，进一步提出了混合维度网格算法HDG，其在二维网格的基础上进一步引入了一维网格，然后结合一维网格和二维网格一起去回答范围查询。

TDG和HDG算法由来：一般来说，如果为了捕获属性之间的关联，那么当维度过大时范围查询将难以解决；如果只关注单个属性，那么就无法捕获属性之间的关联。受到CALM算法的启发，TDG和HDG算法都采用二维网格去权衡以上两点。

TDG和HDG算法均由以下三步组成：

1.构建网格
TDG算法：
首先，融合中心根据d个属性得到m = (d,2)个属性对，并将所有用户随机分成m个用户组，每个用户组对应一个属性对；然后，对于每个属性对，融合中心通过将二维域[c]x[c]划分成同样粒度大小的二维单元构建一个二维网格；最后，为了获得每个二维网格中的二维单元中的加噪之后的频率值，融合中心指示对应二维网格中的用户组中的用户使用OLH算法报告其隐私数据所在的二维单元；
HDG算法：
除了构建上述二维网格之外，融合中心还要为d个属性分别构建一个一维网格。因此在HDG算法中，d + (d,2)个，并且用户被划分为同样数量的用户组，且每个用户组对应一个网格（ps：一维网格和二维网格的粒度大小可能不同）；
2.去除负值和不一致性
因为使用了OLH算法保证差分隐私，因此二维单元加噪之后的频率值可能为负值，这就违背了先验知识的非负性；而且，因为一个属性和多个网格相关，因此不同网格中注入在该属性上的噪声频率可能不同，从而导致网格之间的不一致。因此需要在这个阶段去除负值和不一致这两个问题；
3.回答范围查询
TDG算法：
对于一个二维查询Q，融合中心首先找出与Q相关的二维网格G，然后再检查G里的每个二维单元：如果二维单元完全被包含在Q中，那么融合中心就将其加噪后的频率加到查询结果f(Q)中；如果二维单元部分被包含在Q中，那么融合中心就会采用均匀分布假设估计二维单元和查询Q中共同的二维值的频率值总和，并将其添加到f(Q)中；
HDG算法：
对于一个二维查询Q，融合中心首先找出与Q相关的二维网格G，然后再检查G里的每个二维单元：如果二维单元完全被包含在Q中，那么融合中心就将其加噪后的频率加到查询结果f(Q)中；如果二维单元部分被包含在Q中，那么融合中心先确定二维单元和查询Q中共同的二维值，然后再将响应矩阵中对应元素的总和添加到f(Q)中。

4.2网格后处理

4.2.1非负性

这一步采用Norm-Sub方法，其可以使得所有估计值非负，并且所有估计值的总和为1；

Norm-Sub：
1.所有负估计值转换为0；
2.计算所有正估计值的总和与1之间的总差值；
3.通过将总差值除以正估计值个数获得平均差；
4.通过减去平均差更新每个正估计值；
5.重复以上步骤直到所有的估计值都非负。

4.2.2一致性

对于某个属性a，其总共与d个网格相关（1一个一维网格和d-1个二维网格），假设这些网格为{G₁, G₂, … , G_d}，对于整数j ∈ [1, g₂]，定义P_Gi(a, j)为第G_i个网格中第j个单元的频率总和。为了实现P_Gi(a, j)的一致性，需要如下图所示计算加权平均，其中θ_i为P_Gi(a, j)的权重：

依据其他文献，得知当θ_i进行如下设置时，可以得到最优加权平均为：

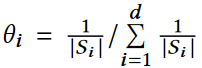
得到P(a, j)之后需要让每个P_Gi(a, j)都相等，可以通过以下方式实现： 对于S_i中的每个单元，通过下图所示的添加变化量来更新其频率：

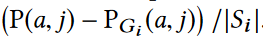
ps：可以发现一致性步骤可能会引入负值，反之亦然。因此在整个网格后处理过程中，需要多次交换执行这两个步骤，而因为响应矩阵的每个元素必须非负，因此以非负性步骤结束网格的后处理。尽管最后一步可能会再次引入不一致性，但其往往很小。

4.3建立响应矩阵

每一个属性对都对应一个大小为[c]x[c]的响应矩阵，其中矩阵中的每个元素代表对应二维值在该二维域中的频率，响应矩阵的建立如下图所示：

算法描述：
1.将响应矩阵中的[c]x[c]个元素都初始化为1/c^2；
2.对于每个二维单元S，将S中所有二维值的频率求和得到总频率Y；
3.将单个二维值的频率除以Y得到该二维值的频率；
4.重复2-3步直到收敛（收敛的标准为：每次更新过程之后响应矩阵中所有元素的改变总和低于一个给定的阈值）

4.4λ维范围查询

为了估计λ维范围查询Q的结果，融合中心首先将Q分成（λ，2）个相关的二维查询，并获取所有二位查询的结果，最后融合中心使用这些二位查询结果去估计f(Q)，下图给出了λ维范围查询结果的估计算法：

4.5隐私和效用分析

4.5.1隐私保证

TDG和HDG算法都满足LDP，因为用户通过OLH算法上传其数据至融合中心，且没有泄露其他信息。

4.5.2误差分析

噪声和采样误差：

一方面，为了满足LDP隐私保证，需要对每一个单元注入一定的噪声，这便引入了噪声误差。而因为对每个单元的噪声注入都是唯一的，因此这些噪声就相当于一些独立随机变量，那么这些噪声总和的方差等于所有噪声方差的总和，所以单元分的越精细，注入噪声的方差就会越大；另一方面，需要使用某个用户组中单元的频率去代表整个人口的频率，但可能当前选择的用户组与全局的的分布不同，这就会引入采样误差；

不均匀误差：

不均匀误差是由与查询矩形相交但不完全包含在其中的单元引起的。 对于这些单元一般需要假设数据点是均匀分布的，而这会在数据点不均匀分布时导致非均匀误差。 通常，任何相交单元格中此误差的大小取决于该单元格中数据点的数量，并受其限制。 因此，分区粒度越细，不均匀误差越小。 计算精确的非均匀性误差需要真实数据分布的可用性，这在我们的设置中并非如此。 因此选择计算近似的不均匀误差；

估计误差：

由于估计误差取决于数据集，因此没有用于估计它的公式。 一般来说，二维范围查询的更准确的答案可以导致更小的估计误差。 但是，其大小取决于数据集的特点会引入不确定性，这意味着在少数情况下可能会出现相反的结果。

4.6选择粒度

基本准则：

为了最小化误差，一维网格的粒度如下图所示：

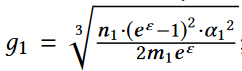
二维网格的粒度如下图所示：

其中n_i是i维网格的用户数，m_i是i维网格的用户组数，α₁、α₂为依赖数据集的常数。

对于g1的分析：

对于一维查询，当粒度为g₁时，平均情况下大概有g₁/2个单元被包含在查询中，那么噪声和采样误差为：

不均匀误差与与查询区间两侧相交的单元中值的频率之和成正比。 假设对于某个常数α₁，不均匀误差为α₁/g₁，那么它的平方误差为(α₁/g₁)²；

综上，为了最小化误差总和和，因此g₁根据如下表达式进行设置：

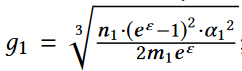
对于g2的分析：

从一维拓展到二维，当二维粒度为g₂时，平均情况下大概有(g₂/2)²个单元被包含在查询中，那么噪声和采样误差为：

不均匀误差与落在查询矩形四个边缘上的单元中值的频率之和成正比。查询矩形的边包含4 x (g₂/2) = 2g₂个单元； 并且这些单元中包含的值的预期频率总和为2g₂ x (1/(g₂ x g₂)) = 2 / g₂。 与一维网格设置类似，假设平均情况下不均匀误差是其中的一部分。 那么对于某个常数 α₂，不均匀的平方误差为(2α₂ / g₂)²；

综上，为了最小化误差总和和，因此g₂根据如下表达式进行设置：