Answering Multi-Dimensional Analytical Queries under Local Differential Privacy

摘要

该文献主要研究LDP下回答多维分析查询的问题（MDA），并提出了几种LDP编码器和频率估计算法去处理不同类型的MDA查询。该文献提出的技术能够在严格的误差范围内回答MDA查询，并在真实数据集和合成数据集上进行了相关实验进一步验证了理论分析结果。

1.介绍

1.1数据模型和应用场景

用户在使用云服务的过程中会产生一些多维数据，这些多维数据大致可以分为以下三部分：measure attributes、sensitive、non-sensitive。另一方面，云服务提供商希望能够在sensitive受到约束的情况下回答一些聚合measure的分析查询，以分析云服务的执行情况。尽管用户所有维度的数据不会全部公之于众，并且上述的分析过程在服务器端内部执行，但是云服务提供商需要提供一个运行在每个用户设备上的LDP数据收集算法，以确保sensitive维度得到妥善处理。

该文献研究的是如何（近似）回答一类多维分析查询（MDA），同时通过LDP收集每个用户的敏感数据。MDA查询就是对measure attributes进行聚合（COUNT, SUM, AVG）的SQL查询，且其约束条件（点约束和范围约束）作用在sensitive上。

1.2解决方案概述

客户端：每个用户拥有一些多维数据，他们使用LDP编码算法A对sensitive进行扰动，并将扰动后的数据上传给服务器；

服务器端：从用户那里收集到进行LDP编码后的数据，然后再将其与其他服务器已知的数据和一些非敏感数据组合共同构成fact table（事实表）。 由于敏感维度是用注入的随机噪声编码的，因此需要一个算法 P 来估计查询结果。

1.3挑战

1.3.1边缘列联表发布

在LDP下回答MDA查询与在LDP下发布边缘列联表（marginal release）的工作密切相关。一个边缘列联表记录了一系列维度之间的概率分布，其中表中的每一行类似于一个COUNT查询。因此可以通过对查询Q覆盖到的边缘列联表中的每一行进行求和来回答一个MDA查询。

挑战：因为表中的每一行数据都被扰动过，即每行数据都带有噪声，那么查询结果每多加一行就会多增加一点噪声，因此该方法存在很大缺陷。一般来说，假设总共有d个有序维度，每个维度有m个不同的值，那么最坏情况下的平方误差会与O(m^d)成正比，而当m很大时，最坏情况的误差可能会非常大。

1.3.2频率估计

在LDP下回答MDA查询与在LDP下进行频率估计（frequency oracle）的工作同样密切相关。这种情景下，客户端每个用户有一个隐私值。此时用户会对敏感数据添加噪声进行LDP扰动， 然后再将扰动之后的数据上传给服务器。而服务器端则需要估计一个给定值的频率。实际上，一些简单的MDA查询（COUNT查询）可以被转换成频率估计问题。

挑战：目前不知道如何通过频率估计解决其他聚合函数（SUM, AVG）的问题，以及如何在多个维度上处理复杂的范围约束条件而不会导致估计误差。

1.4贡献

（1）该文献提出了一种加权频率估计算法：将用户的measure attributes看作用户的权重，然后根据measure attributes对所有用户进行分组，并对每个组的用户个数计数后再将其乘上measure attributes，最后再执行聚合函数（SUM, AVG, STDEV）便完成了MDA查询；

（2）将加权频率估计算法融入到区间分层机制中，使得基于边缘列联表发布的最坏情况下的平方误差从O(m^d)减少到log^O(d)m；并将分解模式从一维扩展到了d维，使得误差仍然为log^O(d)m；

两种方法：一种是将隐私预算基于树的层数的对数级别进行分配；另一种是随机取样，然后将样本的频率估计结果放大为所有用户的频率估计结果；

（3）探究了当整个隐私维度很大但是查询包含的隐私维度很小时误差的优化方案。

2.初步

2.1多维模型和分析

每个用户的多维数据包含的一系列属性（dimensions/measures）构成一个元组t。在一个分析问题中，dimension用D表示，其出现在谓语中，measure用M表示，其出现在聚合函数中，因此t[D]和t[M]代表元组t中的某个属性值（D和M也可以代表属性的取值域domain）。

MDA查询：如下图所示：

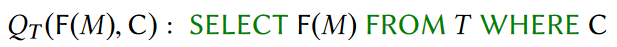
① 聚合函数F(M)可以为COUNT(*), SUM(M), AVG(M)，因为COUNT(*)是一种特殊的聚合函数，且AVG(M)可以从其他两个聚合函数中推导得出，因此主要考虑SUM(M)函数；

② 谓语C由对分类维度的点约束（D_i=v_i）和对有序维度的范围约束（D_i∈[l_i, r_i]）组成。

2.2MDA查询流程

客户端（LDP编码器A）：每个用户采用满足ε-LDP的算法A^ε对其敏感维度进行处理，并将A^ε(t)发送给服务器；

服务器端（估计处理器P）：n个用户的数据元组构成一个事实表T={t₁, … , t_n}，而服务器实际从客户端收集到的表为A(T)={A(t₁), … , A(t_n)}。那么MDA查询q=Q_T(F(M), C)就可以根据A(T)和T的其他属性使用估计算法P近似进行回答，最终得到P(q)；

误差测量：采用期望平方误差Err(P(q))=E[(P(q)-q)²]，如果P(q)是q的无偏估计，那么Err(P(q))=Var(P(q))。

3.加权频率估计

3.1MDA查询的表示

MDA查询的表示方式如下图所示：

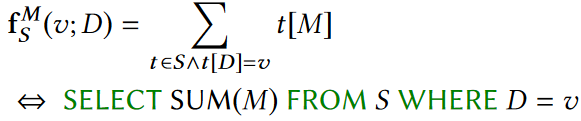
3.2频率估计

3.2.1未加权频率估计（FO）

当所有用户均满足t[M]=1时，MDA查询f^M_S(v)就相当于计算v的频率，即等同于一个COUNT查询：

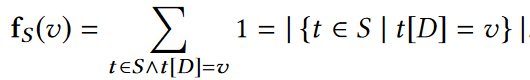
OLH算法是一种拥有渐进最优误差的未加权频率估计算法，其主要流程为：首先从一个哈希函数族中随机选择一个哈希函数H，然后将用户数据中的属性t[D]从范围D映射到一个更小的范围g，并以一定的概率将t[D]扰动为g中某个值y，即y=H(t[D])。因此用户数据t经过LDP扰动后得到的LDP报文为A_FO(t[D])=<H, y>。OLH算法具体流程如下图所示：

Ps：Client side第一步原文作者好像打错了，个人感觉应该是at random

其中，下图所示的引理给出了OLH算法的渐进最优误差：

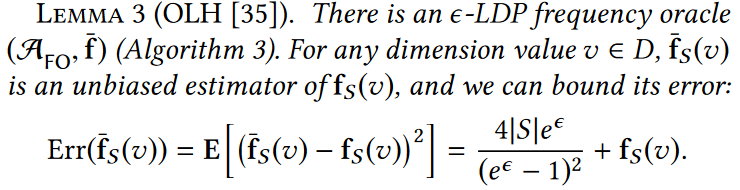
3.2.2加权频率估计（WFO）

为了解决MDA查询，加权频率估计算法在OLH算法的基础上进行了相应调整，该算法的主要思想为将用户根据其measures进行分组，例如S_x={t∈S|t[M]=x}。对于一个维度值v，通过S_x建立FO与WFO之间的关系，如下图所示：

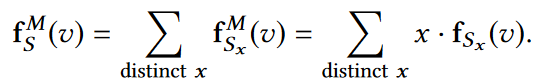
加权频率估计算法的误差推导如下所示：

3.3随机样本放大

当只有某些随机样本被抽取去使用A_FO报告他们的私人值t[D]时，这种情况下首先需要使用f^M估计该样本中值v的加权频率，然后再将所估计的频率放大到所有用户。

Ps：这一做法被作者使用在其所提出的SC机制中，实验指出该做法提升了性能

具体来说，对于用户集合S，首先随机地将S分成S₁, … , S_k总共k个组（其中S中的每个用户以概率1/k随机选择一个组S_i）；然后，只对一个样本（记作S₁）运行加权频率估计算法(A_FO, f^M)，那么就可以得到S₁这个组中v的频率估计，然后再放大k倍即可获取整个用户集合S中v的频率估计：

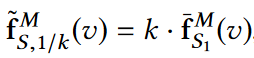
据下图可知，上图式中等号左边的表达式是f^M_S(v)的无偏估计：

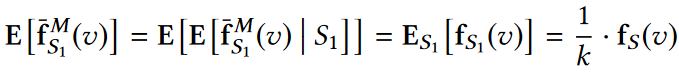
误差：该算法误差有两个来源，一个是来自LDP噪声，另一个是来自采样过程。下图推导了该算法的误差界限：

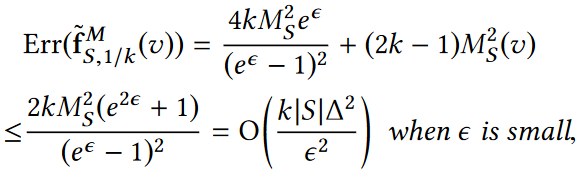
3.4通过边缘列联表回答MDA

估计边缘列联表的机制主要关注COUNT查询，但实际上只需要做一些变换就可以用这些机制去处理MDA查询：为了回答一个MDA查询，首先要根据measure M将事实表T分为多个子表T_x，即T_x={t∈T|t[M]=x}；然后再根据估计得到的边缘列联表去计算每一个子标T_x中的满足限制条件C的元组（记作n_x），那么对于一个SUM类型的MDA查询，其结果可以通过Σ_x x n_x进行求得。

不足：如1.3.1所述，该方法会引入较大的误差。一般来说，假设D∈[l, r]中有m个不同的值，那么根据3.2.2该机制的误差为（线性依赖于m）：

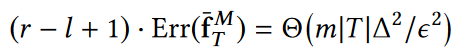
解决方案：为了解决上述问题，4-5节提出了新的机制，使得最终的误差对数依赖于m。

4.单隐私维度分析查询

4.1区间分层机制

4.1.1区间分层

假设有序维度D有m个不同的值，顺序依次为Z₁, Z₂, … , Z_m，然后构建一颗完全B叉树，直到最后一层每个结点只包含一个值：第一层为L⁰={[Z₁, Z_m]}，其对应根节点；最后一层为L^h={[Z₁, Z₁], … , [Z_m, Z_m]}。记I_D={L⁰, … , L^h}，其中h=log_bm。

4.1.2通过区间分层重写查询

对于某个查询q=Q_T(SUM(M), D∈[l, r])，平均来说区间[l, r]可以被分解为2(b-1)log_bm个不相交的子区间I¹, … , I^p。因此查询q便可以相应地分解为基于这些子区间的子查询，而每一个子查询又可以通过加权频率估计算法进行频率估计，如下图所示：

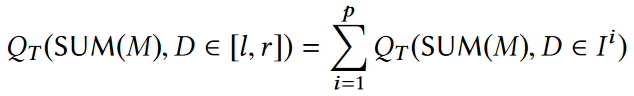
Ps：2(b-1)log_bm来源于普渡大学李宁辉教授的某篇文献（目前还没找到具体文献）

4.1.3HI机制（一维）

客户端：首先隐私预算ε基于完全树的高度h均等地分成h份，那么每一层的隐私预算为ε/(log_bm)，然后用户对其敏感属性所在的每一层的对应区间都使用OLH算法进行LDP扰动，并将扰动之后的树发送给服务器；

服务器端：首先将查询范围D进行重写，然后使用加权频率估计算法去估计每一个子查询，最后再进行求和，那么所得到的求和结果就是查询结果，如下图所示：

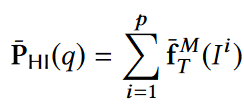
误差：根据以下理论可以得出HI机制的误差界限（根据3.3.2的误差推导出）：

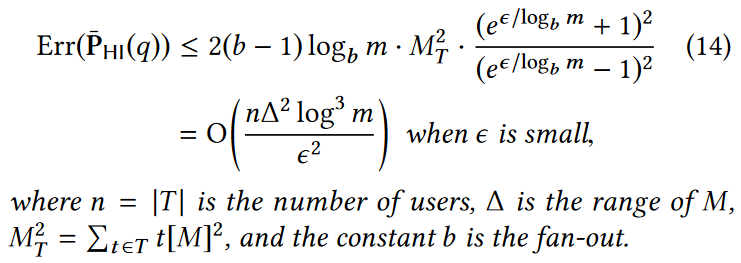
4.2HIO机制（一维）

HIO机制采用3.3节的随机采样放大算法。在HI机制中，客户端将隐私预算对每一层进行平均分配；而在HIO机制中，则采用将用户随机分成h组（h为树的高度）：分组S_j中的用户（对应树的第j层）可以被看成是从整个用户集合S中以采样率1/h得到，且S_j中的用户消耗所有的隐私预算，HIO机制具体如下图所示：

算法流程：和HI机制一样，查询q=Q_T(SUM(M), D∈[l, r])仍然分解为多个子查询；而对于每个子查询所在的子区间的层数，那么就可以使用被分组到该层的用户进行分组频率估计，然后再放大h倍作为该子查询的结果；

误差：根据以下理论可以得出HIO机制的误差界限：

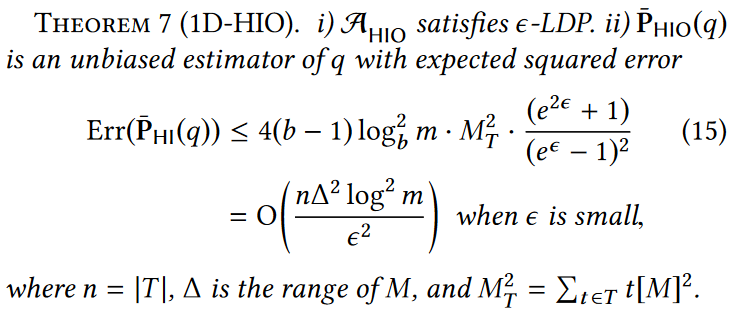
5.多隐私维度分析查询（MDA）

5.1有序维度+有序维度

5.1.1多维度区间分层

二维：二维区间定义为两个一维区间的笛卡儿积，如下图所示：

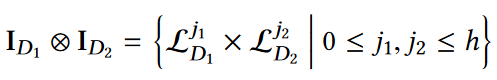
一般来说，区间[l₁, r₁]可以分解成p₁个不相交的子区间，区间[l₂, r₂]可以分解成p₂个不相交的子区间，那么查询q便可以如下图所示进行分解：

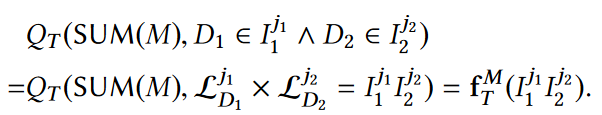
d维：根据二维查询的分解方式，可以得到下图所示的d维查询的分解方式：

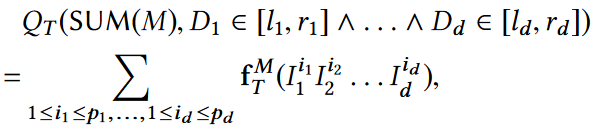
5.1.2HI机制（多维）

算法流程：多维HI机制流程如下图所示：

误差：多维HI机制误差分析如下图所示：

5.1.3HIO机制（多维）

算法流程：多维HIO机制流程如下图所示：

误差：多维HIO机制误差分析如下图所示：

5.2有序维度+分类维度

对于某个分类维度D，可以将其看作成一颗只有两层的树：第一层为一个包含所有取值的根节点，第二层则根据D中不同的值分解为多个只包含一个维度值的结点。通过这种分解转化，那么分类维度同样可以被看作成有序维度去处理。

5.3SC机制

可以看到HI机制和HIO机制所产生的误差随着查询维度数量d_q和总隐私维度数量d的增长呈现指数级增长，于是作者想探究当查询维度数量d_q远小于总隐私维度数量d时，是否可能去除误差对总隐私维度数量d的依赖。

主要思想：与HI机制不同的是，SC机制对d个隐私维度独立编码和上传，那么这种情况下就需要考虑如何将所有独立上传的维度串联起来去完成多维度查询。

5.3.1状态变量及其转移

作者根据下图定义了输入状态和输出状态：

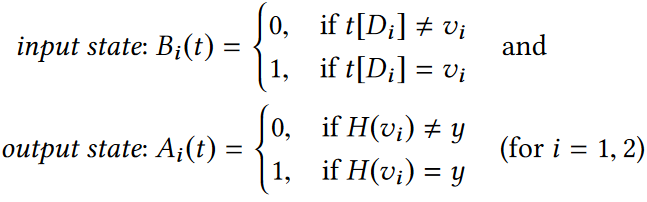
根据输入状态和输出状态便可以定义下图所示的一维转移概率：

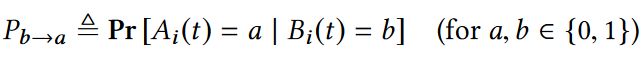
依次类推，便可以定义下图所示的二维转移概率：

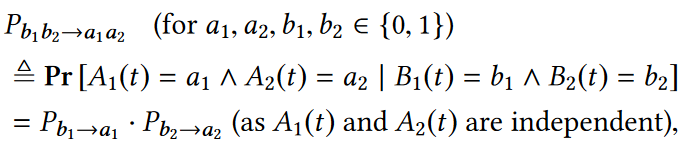
5.3.2通过转移矩阵进行频率估计

主要思想：根据用户集合S及其LDP报文便可以得出每个二维输出状态的频率，然后借助转移矩阵便可得出每个二维输入状态的频率（其中还可以采用加权频率估计算法），如下图所示：

转移矩阵是确定的，使用OLH算法可以求出转移矩阵每个元素的值

多维：二维与多维唯一的区别在于转移矩阵的大小发生了变化，当隐私维度是d维时，转移矩阵的大小为2^dx2^d。

频率估计器误差：如下图所示：

5.3.3SC机制

算法流程：多维SC机制流程如下图所示：

误差：多维HI机制误差分析如下图所示：