Locally Differentially Private Analysis of Graph Statistics

发表于 2022-10-03 分类于差分隐私（英文文献）阅读次数：本文字数： 7.1k 预计阅读时长 ≈ 12 分钟

摘要

图的差分隐私分析广泛用于从敏感图中发布数据并同时能保护用户隐私，但是大部分现有算法采用的是集中式的隐私模型，而这种模型由于服务器的可信赖性和数据泄露的可能性引起了大量的隐私和安全问题。本文提出了一种在本地差分隐私模型下计算子图个数的算法：

对于三角形计数：提出了使用一轮交互和两轮交互的算法，结果表明两轮交互的算法可以提升效用；
对于k-star计数：提出了在非交互式环境下实现最优估计误差的算法；

同时，本文对三角形个数和k星型个数等一般的图数据的估计误差提出了新的下界。最后，在两个真实数据集上进行了大量的实验，最终结果表明，在本地差分隐私模型中准确估计子图个数确实是有可能的。

1. 介绍

1.1 社交网络图

从社交网路图中可以分析得出一些图的性质，以下是社交网络图的几个基本性质：

average degree：即连接到某节点的边的个数，可以用来揭示平均连接性；
subgraph counts：如三角形、星形、团的个数，可以用来衡量聚类系数等中心属性；
clustering coefficient：表示一个人的两个朋友也会成为朋友的概率，其大小影响网络上的传播动力学，当其他参数不变时，平均节点聚类系数越大，传播越慢。

1.2 主要挑战

本文主要考虑两种最基本的连接属性：子图计数和聚类系数：

三角形：计数时不考虑自同构的情况；
k-star形：一个中心节点连接着k个其他的节点；
聚类系数：
$$
3 * triangles/2-stars
$$

主要挑战：

在本地差分隐私模型中计算子图个数不能直接采用现有的对于表格式数据的算法和分析。现今本地差分隐私的研究内容主要集中于表格式数据，而缺乏对图这样复杂数据的研究；
表格式数据假定每个用户的数据是独立的，而在图数据中每个子图都是相互存在联系的。用户的这种相互依赖性成为了作者的算法思想来源：用户和服务器之间的额外交互可能会有所帮助。

1.3 本文贡献

对于三角形计数，给出了两个算法：算法一基于随机相应和经验估计；算法二基于用户和服务器额外的一轮交互，同时为每个算法给出了估计误差的上界，结果表明算法二可以有效减小估计误差；
对于k-star形计数，基于拉普拉斯机制给出了一个简单的算法，并分析了该算法的估计误差的上界，结果表明在所有只采用一轮交互的LDP机制中，该算法在用户数量上是顺序最优的；
对本地模型中一般的图函数给出了估计误差的下界，这比集中式差分隐私中已知的上界更强，然后阐述了局部模型相对于集中式模型的一些限制；
在两个真实数据集上估计了本文提出的算法，结果表明在本地模型中准确估计子图个数确实是可能的，而且本文提出的算法当用户数量很大时估计误差也很小。

2. 相关工作

图DP
- 集中式模型：这种模型中已经提出了很多算法，如子图计数，度分布，特征值和特征向量，合成图等；
- 本地模型：这种模型中算法提出了很多算法，但是很少有关注子图计数的工作；
  - Haipei Sun等人基于一个假定提出了一个在本地模型中计算子图个数的算法，即每个用户允许他的朋友知道其整个好友列表。但这种假定在许多实际场景中是不可能成立的；
  - Qingqing Ye等人基于对邻接矩阵采用随机响应机制提出了估计聚类系数的一轮交互算法。但是该算法在三角形计数中引入了很大的偏差，该团队之后发的一篇文章减小了该偏差，但是他们提出的新方法引入了一些近似值，而这些近似值不能确定是否是无偏的。
LDP
- 如上所述，现今LDP的研究主要针对表格式的数据进行数据分析和频繁项集挖掘，这些研究内容基本不考虑图数据中用户之间复杂的依赖关系；
上界/下界
- 同样由于现有的LDP研究主要针对于表格式的数据，其假定每个原始的数据值都是从一个隐含的分布中独立采样得出的，因此这些研究中提出的上下界不适用于本文的图场景（在图中每个三角形和k-star都不是独立的，其与很多边都存在关联）。

3. 初步

3.1 图和DP

图
- n：用户（节点）数量
- d_max：最大度
DP分类
- 根据隐含结构：
  - 集中式DP
  - LDP
- 根据研究数据（如果是图数据）：
  - edge DP：两个邻居图只有一条边不同；
  - node DP：两个邻居图相差一个节点（从图G中去除一个节点及其邻接边就得到了邻居图）
ε-edge centralized DP
Note:
- 如果两个邻居图中有k条边不同，那么隐私预算就为kε
- 集中式模型中的edge DP是两个邻居图，注意与下面的本地模型中的edge DP相区分

3.2 LDP

采用差分隐私保护用户数据一个首要原则就是需要先想清楚我们具体要保护用户的什么数据。对于图数据来说，本文考虑以下两种本地模型下的edge DP：edge LDP和relationship DP。

3.2.1 Edge LDP

edge LDP的定义基于用户的邻居列表。图G可以用邻居列表表示为a₁, … , a_n，其中a_i是邻接矩阵的第i行，且a_i=(a_{i, 1}, … ,a_{i, n}) ∈ {0, 1}ⁿ，其具体定义如下：

3.2.2 Relationship DP

在社交网络图中，通常两个用户会共享他们之间边的存在性信息，为了隐藏这条相互边，必须考虑两个用户的数出都可能泄露信息，因此本文提出了relationship DP。relationship DP定义如下：

3.2.3 各种DP间的区别

egde LDP与relationship DP：egde LDP将同一条边v_i<->v_j在节点v_i和在节点v_j中看作是不同的信息，而在relationship DP中则认为两者相同；
LDP与relationship DP：因为LDP中的每条用户数据都与其他数据相互独立，因此用户可以相信其他用户不会泄露自己的任何信息，而relationship DP研究的彼此存在相互依赖的图数据，因此只有花费隐私预算才能保证这一点，所以relationship DP的隐私保证比LDP更强；
DP与relationship DP：从两者的定义可以看出，DP是对真实值进行扰动，而relationship DP的隐私保证比DP更弱，因为在DP中服务器需要花费更多的隐私预算来保护用户的隐私数据。

3.2.4 Edge LDP与Relationship DP的关系

edge LDP与relationship DP的关系如下图所示：

该定理说明，当我们需要将一条边作为一个整体进行保护时，隐私预算的开销需要加倍。考虑到该问题，本文提出了一些没有隐私开销加倍问题的随机算法：

主要思想
- 因为社交网络图可以用对称的邻接矩阵表示，因此考虑只对下三角矩阵进行扰动，从而去除了开销加倍的问题；
具体做法
- 使用随机响应算法对用户i的邻居列表a_i进行扰动时，只对v₁, … , v_i-1进行扰动，因此随机算法(R₁, … , R_n)可以完成下三角矩阵的扰动过程，进而保护整个图数据，同时随机算法(R₁, … , R_n)的整个开销预算为ε。

3.3 全局敏感度

因为采用拉普拉斯机制去实现edge centralized DP和edge DP，所以需要考虑全局敏感度，其定义如下：

图中的全局敏感度可能会特别大，例如，在图中增加一条边可能会导致三角形的个数增加n-2（将新增的边作为新产生的三角形的一条边，那么再从剩下的n-2个节点中任意选出一个节点就可以构建一个三角形），k-star的个数增加2C_n^k-1（分别以新增的边的两个节点为k-star的中心，那么还需要从剩下的n-2个节点中选出k-1个节点就可以构建一个k-star）。一种降低全局敏感度的有效方法是采用graph projection，即从邻居列表中去除一些邻居从而使得最大度d_max可以以一个预定值$\widetilde{d_{max}}$<<n作为其上界，这种方法使得当在图中增加一条边时三角形的个数最多增加$\widetilde{d_{max}}$，k-star的个数最多增加C_{$\widetilde{d_{max}}$}^k-1。

一般选取最大度d_max作为$\widetilde{d_{max}}$的值，这样可以避免从邻居列表中去除邻居。然而最大度d_max可能会泄露原始图的隐私信息。因此在本文中采用了一种差分隐私随机梯度下降的自适应裁剪算法：先通过edge LDP估计出d_max的值，然后再将该值设置为$\widetilde{d_{max}}$的值。

3.4 图数据和效用衡量

图数据
- 本文考虑一类图函数：以图G作为输入，输出三角形，k-star的个数和聚类系数等图数据；
效用衡量
- 本文使用均方误差（l₂ loss）和相对误差进行效用衡量。

4. 算法

4.1 模型构建

一轮交互模型
- 服务器给用户v_i发送一次查询R_i，然后用户v_i单独发送其回答R_i(a_i)给服务器；
多轮交互模型
- 服务器给用户v_i发送多次查询R_i，然后用户v_i单独发送其回答R_i(a_i)给服务器，这种模型可能使得可能查询得到更准确的图统计数据；

4.2 k-star的一轮交互算法(LocalLap_k*)

4.2.1 算法描述

k-star的一轮交互算法(LocalLap_k*)具体如下图所示：

k-star的一轮交互算法(LocalLap_k*)
输入：用邻居列表(a₁, … , a_n)表示的图G，隐私预算ε，$\widetilde{d_{max}}$；

输出：k-star图形个数的估计值；

算法流程：

初始化$\triangle$

对每一个邻居列表进行如下操作：

将邻居列表进行映射，即限定节点的邻居数量必须 <= $\widetilde{d_{max}}$；

映射完毕后计算节点的度数；

计算以当前节点为中心的k-star图形的个数r_i；

将r_i添加拉普拉斯噪声然后发布；

将所有r_i值进行求和并返回总和。

4.2.2 算法理论证明

LocalLap_k*算法满足以下两个理论：

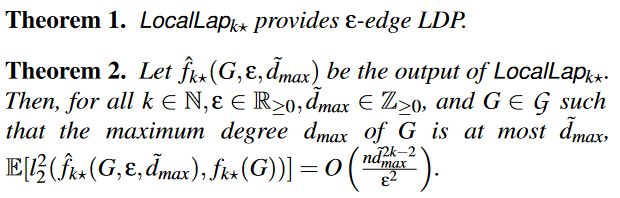
由于LocalLap_k*对邻居列表添加拉普拉斯噪声的总次数为n，所以复杂度中存在n；而在集中式模型中因为是对k-star总和进行加噪，所以复杂度中没有n。

在edge centralized DP模型中f_k*的敏感度为2C_{$\widetilde{d_{max}}$}^k-1，因此本文在实验过程中增加了一个CentralLap_k算法，其对k-star的真实值f_k(G)添加一个拉普拉斯噪声，即CentralLap_k算法的输出值为：f_k(G)+Lap(2(C_{$\widetilde{d_{max}}$}^k-1)/ε)。

4.2.3 关于n的推论

一轮交互算法中n存在以下推论：

本文在实验中发现当n很大时LocalLap_k*算法仍然能准确的估计f_k(G)。而且，随着n的增大相对误差也逐渐减小。

4.2.4 d_max的估计

考虑到真实的d_max值可能会泄露隐私信息，因此需要增加一轮交互过程，具体算法过程描述如下：

将隐私预算ε分解为两部分，ε = ε₀ + ε₁，ε₀用于获取d_max，ε₀用于对k-star的个数值进行加噪；

然后服务器向每个用户发出询问，得到每个用户节点的度数，并据此得到最大度d_max，然后对其利用隐私预算ε₀对其进行加噪，并发布给所用用户节点；

最后再利用隐私预算ε₁执行LocalLap_k*算法并发布最终的k-star个数。

可以看到两轮交互的算法同样提供ε-edge LDP的隐私保证。

4.3 三角形的一轮交互算法(LocalRR_$\triangle$)

4.3.1 算法思想

该算法的思想就是随机响应RR和经验估计。值得注意的地方是服务器在拿到扰动后的用户数据时，此时如果直接计算三角形的个数，那么得到的结果将会是一个有偏的估计值。所以需要采用以下引理获取f_$\triangle$G的无偏估计值：

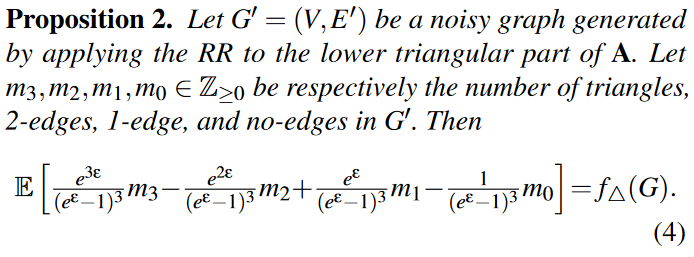
4.3.2 算法描述

三角形的一轮交互算法（LocalRR_$\triangle$)算法具体如下图所示：

三角形的一轮交互算法(LocalRR_$\triangle$)

输入：用邻居列表(a₁, … , a_n)表示的图G，隐私预算ε；

输出：f_$\triangle$G的估计值；

算法流程：

每个用户v_i使用隐私预算ε对其邻居列表(a_{i, 1}, … , a_{i, i-1})进行扰动，然后发布其扰动之后的邻居列表(RR_ε(a_{i, 1}), … , RR_ε(a_{i, i-1}))；

服务器根据所有用户上传的扰动之后的邻居列表及无向图的对称性去构建一个无向图G’；

服务器从无向图G’中数出m₀, m₁, m₂, m₃的个数，并使用公式(4)计算f_$\triangle$G的无偏估计值，最后返回该无偏估计值。

4.3.3 算法理论证明

LocalRR_$\triangle$算法满足以下两个理论：

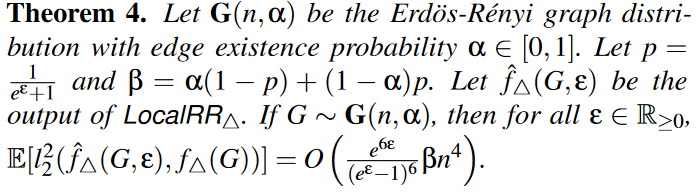
本文在实验过程中增加了一个CentralLap_$\triangle$算法，其对三角形个数的真实值f_$\triangle$G添加一个拉普拉斯噪声，即输出值为：f_$\triangle$G + Lap($\widetilde{d_{max}}$/ε)。

4.3.4 误差分析

LocalRR_$\triangle$算法的误差来源于三角形的每条边都是以某种被翻转的概率独立上传，即三条边相当于图G’中的三个随机变量。

4.4 三角形的两轮交互算法(Local2Rounds_$\triangle$)

4.4.1 算法思想

显然，如果只采用一轮交互，那么每个用户不可能知道是否存在三角形，但是如果增加一轮交互，即在第一轮交互之后，服务器发布加噪之后得到的无向图G’，用户可以根据无向图G’去判断第三条边的存在性。这样每个用户就可以数出三角形的个数。同样值得注意的是，计算得出的无向图G’中三角形的个数肯定是无偏的，因此需要根据以下引理进行计算，从而得到一个f_$\triangle$G的无偏估计值：

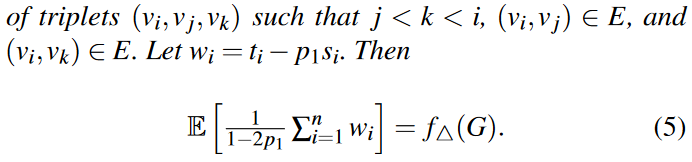
4.4.2 算法描述

三角形的两轮交互算法(Local2Rounds_$\triangle$)具体如下图所示：

三角形的两轮交互算法(Local2Rounds_$\triangle$)

输入：用邻居列表(a₁, … , a_n)表示的图G，两个隐私预算ε₁, ε₂，$\widetilde{d_{max}}$；

输出：f_$\triangle$G的估计值；

算法流程：

每个用户v_i使用隐私预算ε对其邻居列表(a_{i, 1}, … , a_{i, i-1})进行扰动，然后发布其扰动之后的邻居列表(RR_ε(a_{i, 1}), … , RR_ε(a_{i, i-1}))；

服务器根据所有用户上传的扰动之后的邻居列表及无向图的对称性去构建一个无向图G’，同时将无向图G’发布；

每个用户收到无向图G’之后，首先将邻居列表进行映射，即限定节点的邻居数量必须 <= $\widetilde{d_{max}}$，然后数出t_i和s_i的个数，并根据上述引理得到w_i，然后再使用拉普拉斯机制对w_i进行加噪处理，最后将其发送给服务器；

服务器收到每个用户的w_i后，采用上述引理得到f_$\triangle$G的估计值，最后返回该无偏估计值。

4.4.3 算法理论证明

Local2Rounds_$\triangle$算法满足以下两个理论：

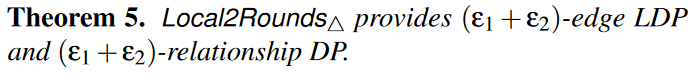
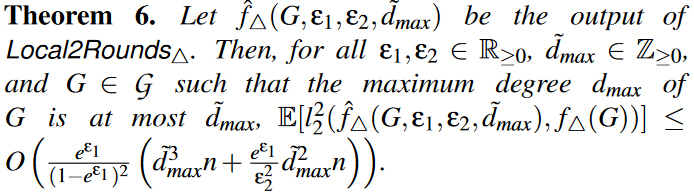
从第二个理论中可以看出，通过增加一轮交互，均方误差从O(n⁴)减小到了O($\widetilde{d_{max}^3}$n)。

4.4.4 d_max的估计

上面的Local2Rounds_$\triangle$算法将d_max作为其输入，但是并没有提及其获取方式。实际上，在Local2Rounds_$\triangle$算法中采用与LocalLap_k*同样的获取方式。具体来说，可以将隐私预算ε分成三份，即ε = ε₀ + ε₁ + ε₂。在第一轮交互过程中，每个用户使用ε₀上传加噪之后的度d_i，同时需要使用ε₁上传其加噪之后的邻居列表；在第二轮交互过程中，服务器首先根据每个d_i获取最大度d_max，然后再进行之后的操作。

总体来说，整个算法提供(ε0 + ε1 + ε2)-edge LDP和(2ε0 + ε1 + ε2)-relationship LDP。

4.4.5 时间复杂度和通信开销

时间复杂度
- LocalRR_$\triangle$算法是低效的，因为该算法需要从G’中数出三角形的个数m₃，而在图中总共有C³_n个包含三个节点的子图，因此该过程的时间复杂度为O(n³)；
- 相反，Local2Rounds_$\triangle$算法的时间复杂度为O(n² + nd²_max)。其中n²是由于无向图G’的大小为n²。
通信开销
- 每个用户需要根据无向图G’去数出t_i和s_i的个数，这肯定会导致O(n²)的通信开销。但本文没有在实验中估计该算法的通信开销。

4.5 下界

本小节主要探讨在一轮交互模型的所有算法中，复杂度是否中一定包含n，推导结果表明回答是肯定的。

输入图的具体结构定义如下图所示：

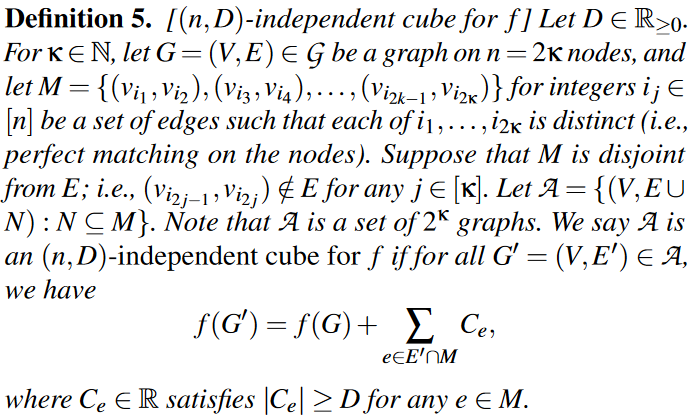
根据上述结构定义，本文给出了下界的证明，如下图所示：

5. 总结

本文提出了在本地差分隐私模型中计算子图个数的算法：具体来说，对于三角形计数，给出了一轮交互算法和两轮交互算法；对于k-star计数，给出了一轮交互算法。同时，本文证明了所有一轮交互算法的时间复杂度一定会包含用户节点个数n。

思考：

两轮交互的三角形计算算法中，每个用户都能获取加躁之后的社交网络图，那么实际上攻击者是可以直接从这个图数出三角形的个数的，如果第二轮加躁之后再把个数上传给服务器，之后服务器再求和，那么这个求和结果与直接从加躁之后的图中数出的结果会不会相差很大？而这个差别会不会带来什么影响？如果存在影响那应该怎么解决？

‌同样是上述算法，在第二轮给三角形个数加躁的过程中，噪声完全覆盖真实值的情况感觉完全有可能发生，那这种情况下会不会导致发布的三角形计数结果误差过大？所以是否可以采用动态调节的思想，当计数小于某个阈值时就不加躁？如果可以的话阈值应该怎么确定？

‌图中的度分布求解发布等问题感觉可以采用边缘列联表发布的方法去解决，是不是可以沿着这个思路尝试一下

摘要