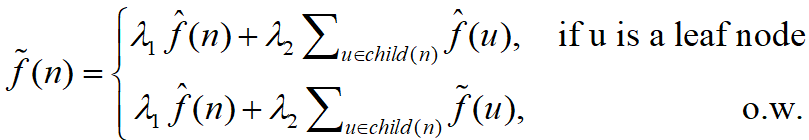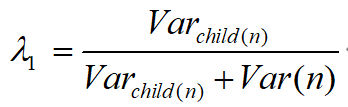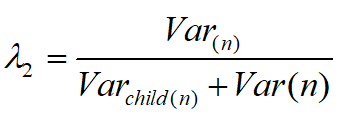AHEAD: Adaptive Hierarchical Decomposition for Range Query under Local Differential Privacy

摘要

为了保护用户的隐私数据，人们使用本地差分隐私（LDP）提供支持隐私保护的范围查询，并支持进一步的统计分析。然而，现有的基于LDP的范围查询方法受限于其属性。而这种静态框架在低隐私预算场景下会带来过量的噪声。因此，提出了AHEAD（Adaptive Hierarchical Decomposition）方案，它可以自适应且动态地控制树的结构，进而注入的噪声可以得到较好地控制。

1.介绍

1.1DP和LDP的执行流程

DP：一个可信的中心聚合器从用户端收集到敏感数据，然后再执行扰动分析，最后通过回答查询或者发布合成数据来提供数据服务；

LDP：用户首先在本地对自己的隐私数据进行编码和扰动，然后再将处理过后的数据传输给聚合器。

1.2LDP的研究

频率估计问题（Frequency Oracle）（即获得整个域的频率分布）是LDP过去的主要研究内容，然而实际上人们可能对范围查询更加感兴趣。而且，根据范围查询结果，我们可以直接获得其他分布特征（如顺序统计量）；

顺序统计量：在一个由n个元素组成的集合中，第i个顺序统计量即为该集合中第i小的元素。

1.3范围查询

范围查询根据查询维度可以划分为低维度查询（维度小于等于2）和高维度查询（维度大于等于2）：

低维度查询：王等人提出了基于完全B叉树结构分层分解整个域并且通过累积频率值来回答范围查询；Cormode等人提出在扰动的时候使用离散小波变换将用户的隐私值转化为一个哈尔变化系数向量并且执行其逆变换得到查询结果；

1.3.1离散小波变换（待续）

1.3.2哈尔小波变换（待续）

高维度查询：杨等人提出从一二维网格组合信息，并且使用加权更新策略去估计高纬度的范围查询。

1.4现有的方法存在的限制

大多数真实世界数据集中的数据域中存在稀疏区域（也就是某些区间的比重可能非常小），因此在网格或完全树中的值较小的结点可能被注入的噪声淹没；

现有的科技主要为具体维度的查询而设计（而实际数据集是经常变化的）（可以理解为都是静态框架），虽然每一种方法技术上不受查询维度的限制，但是在非目标维度的情况下有效性会降低，为了解决维度变化问题，聚合器需要组合为不同维度设计的算法，而这会限制这些算法的适用性和实用性。

1.5文章的贡献

提出了一种在LDP下解决范围查询的动态算法AHEAD，它可以自适应地觉得域组合的粒度大小；

理论上推导了在满足严格的LDP保证下能实现高效用的参数设置；

通过大量实验证实了AHEAD算法的有效性。

2.背景

2.1频率估计（Frequency Oracle）

频率估计是用来估计某个隐私属性的频率分布F，作为一般LDP任务（边际释放和范围查询）的基本构建块。大部分FO算法包括三部分：编码、扰动和聚合。

2.2两种FO协议（GRR和OUE）

2.2.1广义随机响应（Generalized Randomized Response, GRR）

Ps：随机响应算法的广义版本，目前我理解的是先对隐私数据进行扰动再进行编码

编码：对于用户i的隐私数据Vi，将其编码为Xi；

扰动：用户i以根据以下式子选择Vi的值，并将扰动后的隐私值对应的编码Xi'上传到服务器（其中Vi'是从数据集D中随机选择）；

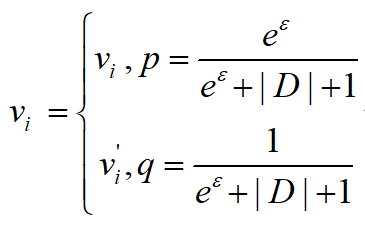
聚合：聚合器首先收集所有经过用户扰动之后的数据，然后计算每个数据V的频率count[V]，count[V]的一个无偏估计为：

估计误差：GRR的估计误差源自算法方差：

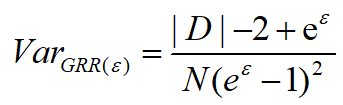
2.2.2优化的一元编码（Optimized Unary Encoding, OUE）

Ps：RAPPOR算法的优化版本

编码：对于用户i的隐私数据Vi，采用独热编码的方式将其编码为一个长为长度|D|的向量，其中Vi数据对应向量的第i个值为1，其余均为0；

2.2.2.1One-Hot Encoding（独热编码）

One-Hot编码，又称为一位有效编码，即采用N个独立的寄存器对N个状态进行编码，对于每个状态，只有一个寄存器的值为1，其余寄存器的值都为0

扰动：对上一步得到的每个数据都采用GRR方法进行扰动，具体对每个数据的每一位来说，如果该位为1（0），则以概率p（q）保持不变，以概率1-p（1-q）进行反转，然后用户将扰动后的编码Xi'传输到服务器

聚合：聚合器收集到所有经过用户扰动后的数据，然后对每一位为1的个数进行频率统计得到count[V]，count[V]的一个无偏估计为：

估计误差：算法方差为：

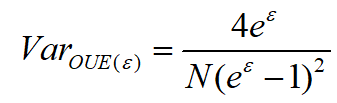
总结：可以看到，GRR和OUE算法都得到了频率值的无偏估计，而且，OUE算法的方差独立于数据集大小|D|。所以对于更小的|D|，GRR算法更好；而对于更大的|D|，OUE算法更好

3.现有的解决方案（针对范围查询问题）

3.1Hierarchical-Interval Optimized（HIO）

3.1.1算法描述

基于B叉树，HIO算法将整个域分层分解为相互不相交的子集称为区间。根节点代表整个域，叶节点代表单个的值，其中相同层的结点代表相同粒度的区间。HIO算法通过OUE算法获得每一层结点的频率估计值，且通过使用最少的来自不同层的区间来回答范围查询。

对于范围长度为r的一般查询，HIO算法最多需要2（B-1）log_B|D|个区间进行回答

3.1.2算法不足

在所有区间的估计频率值中插入了相同级别的噪声，对于小区间的结点，扰动噪声可能会淹没真实的频率值，进而降低了整个算法的有效性；

在多维度场景中，树的层数随着维度的变化呈指数级增长；

在高维度场景中，查询误差因为小区间的结点数量过多，查询误差会不断增加。

3.2Discrete Haar Wavelet Transform（DHT）

3.2.1算法描述

DHT算法对于整个域采用采用完全二叉树结构，并且把用户的隐私数据编码为一个哈尔小波系数集合。

对于范围长度为r的查询，DHT算法比起直接采用FO算法能够在哈尔变换域中使用更少数量的估计值

3.2.2算法不足

与HIO算法相似，在所有区间的估计频率值中插入了相同级别的噪声，对于小区间的结点，扰动噪声可能会淹没真实的频率值，进而降低了整个算法的有效性；

主要针对一维场景设计，因此限制了其实际的应用场景。

3.3Consistent Adaptive Local Marginal（CALM）

3.3.1列联表（Contingency table）

列联表：观测数据按两个或更多属性（定性变量）分类时所列出的频数表，是由两个以上的变量进行交叉分类的频数分布表，其分析的基本问题是判明所考察的个属性之间有无关联（即是否独立）。若所考虑的属性多于两个则称为多维列联表。如果考虑集合的全部属性，则称为全列联表；如果考虑集合的部分属性，则称为边缘列联表。若考虑集合的属性个数为k，则称为k-路边缘列联表。

Ps：全列联表就是联合概率密度分布，边缘列联表就是边缘概率密度分布

3.3.2算法描述（有点复杂，待续）

CALM算法是一种满足LDP定义的边缘列联表发布（Marginal Release）方案，它可以在隐私保护保证的背景下构建m个属性的列联表。该算法使用对重构的被包含在查询中的列联表进行求和来对范围查询进行回答。

3.3.3算法不足

当数据集大小|D|很大时，CALM算法在回答一个查询时会加入大量的加噪列联表，而这很可能会给真实值注入大量的噪声。

3.4Hybird-Dimensional Grids（HDG）

3.4.1算法描述

仔细地将属性对的二维域都划分到粗的二维网格中，并且从相关的二维范围查询的答案中估计更高维度范围查询的结果。为了捕获用户数据的细颗粒分发信息，HDG算法还引入了一维网格去提供每个属性上的细粒度分发信息，并将来自一维和二维网格信息结合在一起去回答范围查询。

3.4.2算法不足

相同粒度的网格不能处理用户数据的各种分布；

使用一维网格可能会破坏属性之间的相关性。

3.5附注

3.5.1设计目标

为整个域找到一个合理的分解策略去避免引入过量的噪声；

在拓展到多维场景时，设计的机制应该要比现有算法的有更高的查询精确度。

3.5.2与现有算法的不同之处

AHEAD算法是自适应且动态的算法；

AHEAD算法减少了噪声对小区间结点的影响；

AHEAD算法可以从一维拓展到高维场景中。

4.AHEAD算法

4.1动机和概述

一方面，当回答查询需要结合多个小区间结点时，因为每个区间结点都需要满足LDP的隐私保证，所以都会引入噪声，当小区间结点过多时注入的噪声就会更加地多，为了解决这一问题，因此需要动态地结合不同的区间结点，进而减少注入的噪声量；

另一方面，当查询的范围是某个区间的一部分时，此时需要采用主流的均匀分布假设来回答查询，这时如果区间内分布不均匀就会引入不均匀误差；

综上分析，AHEAD算法应该试图平衡这两种误差，并解决现有算法的不足。

4.2工作流程

4.2.1采样方案的选择（Sampling Principle）

使用隐私预算时有两种策略：隐私预算拆分策略和用户分区策略

隐私预算拆分策略（privacy budget splitting strategy）：将整个隐私预算𝜖分成c份，并且在隐私预算𝜖/c下对所有用户的报告进行频率分布的估计；

用户分区策略（user partition strategy）：随机地将用户分为c组，并使用整个隐私预算从魅族用户那里获取频率值；

对于相同的区间结点，两种策略的方差分别如下所示：

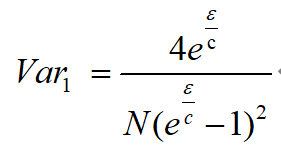
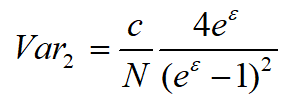
因为𝜖>0且c>1，所以Var1>Var2

Ps：这两个方差的大小比较还没弄明白（待续）

综上，AHEAD算法选择了用户分区策略（user partition strategy）。

4.2.2算法流程

Step1：User Partition：聚合器首先确定用户分区数量c，其中c=log_B|D|，然后用户在[1, 2, ... , c]中随机选择一个分区号（用户也可以使用其公共信息去选择分区号）。分区过程应该确保每个分区拥有相似的用户数量去代表总体人口；

Step2：Noisy Frequency Construction：聚合器首先创建一个根节点n₀代表整个域，然后聚合器对整个域执行初始分解（即把整个域分解成B个大小相等的区间，B是树的分支数），并将分解得到的区间结点指向根节点n<sub>0</sub>，此时根节点n<sub>0</sub>的子结点代表整个域的划分方式E₁。之后聚合器选择第一个分区的用户并将E₁和隐私预算𝜖发送给用户。这时第一个分区的用户就会先扰动自己的隐私数据，并将扰动值通过OUE算法投入到E₁划分后得到的区间中。聚合器在收到用户的数据后就会使用聚合算法去获得频率估计分布F₁；

Step3：New Decomposition Generation：聚合器得到区间的频率估计分布F₁={f₁, f₂}之后，会根据阈值θ决定是否要对区间结点进一步分解。具体来说，如果某个频率f小于阈值θ，则不需要再进行分解；如果某个频率f大于阈值θ，则需要对该区间再次进行分解得到划分方式E₂并处理下一组用户；聚合器重复以上步骤知道所有的用户数据都已经处理完毕。在构造上述的原型树时没有考虑书中频率值的约束（子结点的频率值总和等于父节点的频率值），因此需要进行后处理；

Step4：Post-processing：该步骤包含非负和加权平均（可以最大程度减少噪声的幅度）两步操作。AHEAD算法首先在相同层中通过NormSub算法使得结点的估计频率值都非负，且所有频率值的总和为1；然后自底向上计算非叶节点n和其子结点的加权平均值去更新n的频率估计值（通过结合n的多次估计来减少加性噪声）：

对于非根节点n：

其中，参数设置如下（这样设置可以得到最小的更新方差）：

Var_child(n)代表结点n的子结点的方差总和，Var_n代表结点n的方差。f~代表f^的后处理版本

定理：使用上述方程对子结点进行组合时，结点n可以获得最小的更新方差

证明：（待续）

最后，在结点区间均匀分布的假设下，自顶向下对频率值进行迭代分解以获得一颗用于回答范围查询的完全树，至此，AHEAD算法结束。

4.3隐私和效用分析

4.3.1隐私保证

定理：AHEAD算法满足𝜖-LDP

证明

Step1中，用户在[1, 2, ... , c]中随机地选取其分区，这一步没有隐私预算消耗；Step2和Step3中，AHEAD算法顺序地与用户进行交互，并且每个用户产生一个输出；Step4中，AHEAD算法没有触及用户地隐私数据，因此不会产生额外地隐私预算；因此，如果在和用户交互时（Step3和Step4）满足𝜖-LDP，那么AHEAD算法满足𝜖-LDP；

在每个交互时回合中，AHEAD算法都基于Step2中的隐私预算𝜖使用OUE算法构建嘈杂的频率；对于分区g中同一用户的任何一对可能值v₁, v₂∈D，加噪的二进制向量O为OUE范围内的潜在输出；

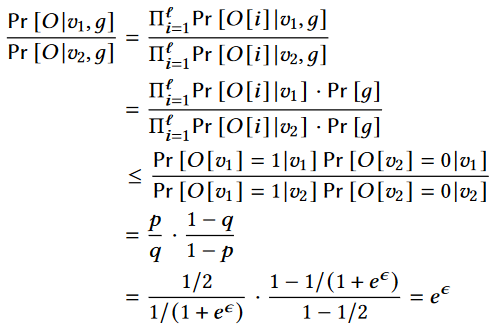
上式中l是O的长度。根据上式可知，Step2满足𝜖-LDP，而由于Step3处理的是用户上传的加噪之后的数据（即没有使用用户原始的隐私数据），所以没有消费额外的隐私预算消费；

综上，AHEAD算法满足𝜖-LDP

4.3.2误差分析

AHEAD算法的误差来源有三个：噪声、采样误差、不均匀误差

噪声和采样误差：来自OUE扰动和用户采样过程。虽然OUE算法可以得到频率估计值的无偏估计，但是仍然会存在由扰动导致的估计方差，而据研究分析，采样误差是一个远小于注入噪声的常数；

不均匀误差：来自于一些区间，其频率值要通过较大的区间（父节点）来获得，而父节点并不一定满足均匀分布假设

综上，AHEAD算法的主要误差为噪声和不均匀误差

4.4B和θ的选择

4.4.1θ的选择

θ遵循以下式子进行设置：

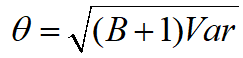
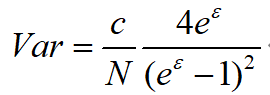
分析

首先使用在HIO算法中使用的策略去获得频率估计值和整体估计误差的期望，具体计算如下：

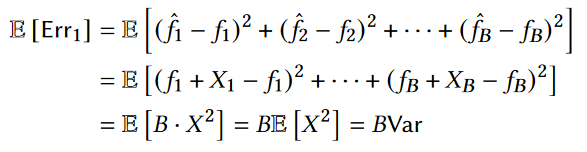
然后使用在AHEAD算法去获得整体估计误差的期望，具体计算如下：

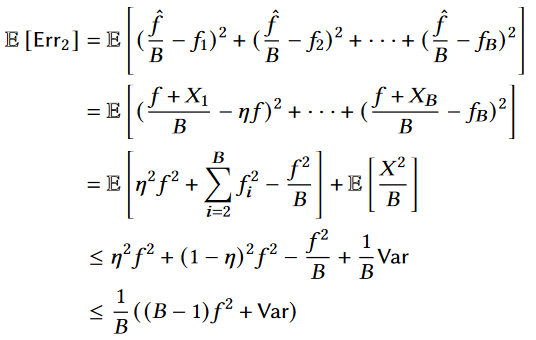
然后令AHEAD算法的误差小于HIO算法的误差，得到以下不等式：

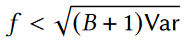
综上，使用上述式子对θ进行设置时可以更好地减小估计误差

4.4.2B的选择

分支因数B的作用在于平衡树的高度和回答查询需要的结点数量，AHEAD算法在考虑了不均匀误差的基础上将B设置为2

分析

因为对数据的分布没有先验知识，所以对于不均匀误差应该考虑最坏情况，此时估计误差的期望为：

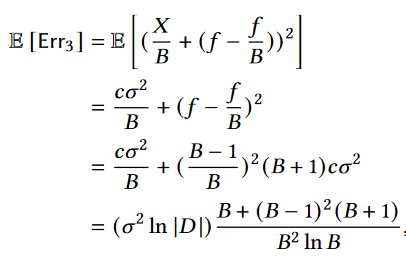
对上式进行求导并另导函数为0，得到B=0.6或B=2.2。因为分支因数为大于1的整数，并且B=2比B=3的期望更小，所以最终设置B=2

4.5拓展到多维场景

4.5.1二维范围查询

对于AHEAD算法，一维和二维的主要区别在于分解过程：对于一维场景，分解的总区间为[1, |D|]；对于二维场景，分解的总区间为[1, |D|]x[1, |D|] ；

对于二维场景，AHEAD算法将B设置为4（每个维度的B=2），其具体的工作流程与一位范围查询基本相同。而为了减小随着结点使用数量不断增加而增加的查询误差，AHEAD算法更偏向于使用粗粒结点来回答查询（即自顶向下）

4.5.2高维范围查询

AHEAD算法可以通过两种方式拓展到更高维度：Direct Estimation、Leveraging Low-dimensional Estimation

Direct Estimation：对于一颗分支因数为B=2^m的树，AHEAD算法同时在m个维度进行分解；该方法的不足在于随着维度的不断增加，叶节点的数量呈指数级增长，这使得对高维度数据集进行范围查询处理时变得相当耗时；

Leveraging Low-dimensional Estimation：该算法对用户数据的数量进行结对组合，并对每一对属性对构建一颗二维AHEAD树；当回答一个m维的范围查询时，LLE构建了一个带有关联2^m个查询的查询集合，然后，以二维频率作为限制，LLE通过最大熵优化估算所有2^m个查询的频率值

最大熵优化估算：（待续）

综上，DE方法的实现相对简单，并且用户分区的数量不会随维度的增加而增加。但是，在高维场景中，使用DE的AHEAD树可能非常大，这会使树的构造和进行范围查询的过程变得相当耗时。与DE相比，LLE将属性成对结合在一起，然后为每个属性对构造一个二维AHEAD树，这会使每棵树的规模都不太大。

5.总结

通过利用自适应层次分解，为一维和多维范围查询问题提出了一种新颖的LDP协议。AHEAD算法满足了严格的LDP保证，同时使用理论上衍生的参数实现了有利的实用性性能。通过理论分析以及广泛的实验评估，文章展示了AHEAD算法在范围查询方面平衡效用和隐私性的有效性及其在最新方法中的显着优势。此外，通过研究各种参数设置，文章得出了几种在实践中采用的重要观察。