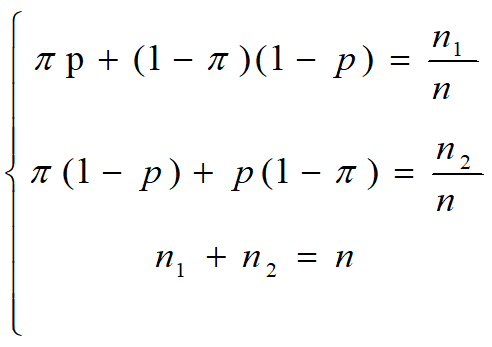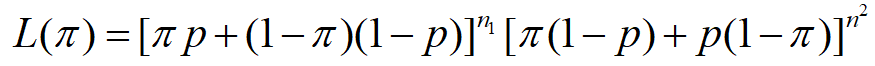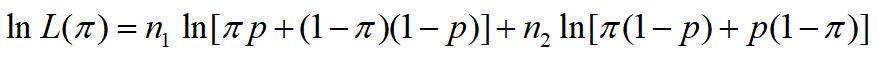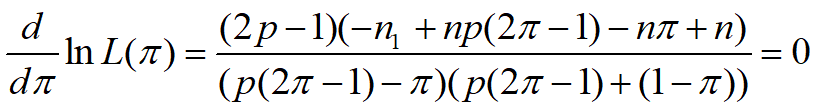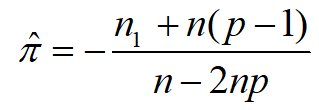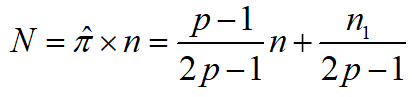本地差分隐私保护综述

1.众包模式

一个公司或机构把过去由员工执行的工作任务，以自由自愿的形式外包给非特定的，而且通常是大型的大众网络的模式

2.隐私保护的目标

在数据收集阶段引入隐私保护机制来降低并控制隐私泄露的风险，平衡隐私保护与数据可用性之间的关系，解决和完善针对不牺牲用户个人隐私的大数据分析问题和机制

3.传统隐私保护算法的缺陷

（1）集中存储模型下，非可信数据管理者使用户无法直接控制个人隐私数据（DP也存在这一问题）

（2）由于背景知识无法明确界定，基于等价类的隐私保护模型被迫随着新攻击技术的出现而不断被动调整（3）无法提供严格且有效的数学理论来证明其隐私保护水平，无法定量分析隐私泄露风险

（4）值得重视的是，即使被严格处理的数据也可能泄露用户隐私

4.本地差分隐私保护（LDP）的优势

本地差分隐私保护可以在不需要信任第三方数据管理者的情况下，直接在本地将隐私数据加噪来保护个人信息不被泄露，同时从宏观角度保证数据收集者可正确地推断出群体统计信息

5.LDP应用场景

（1）集值型流式频繁项集挖掘的Heavy Hitters估计

（2）众包模式下字符串边缘频率估计和联合概率估计

（3）针对智能设备的机器学习

6.布鲁姆过滤器（Bloom Filter）

（1）定义：由一个超长的二进制位数组和一系列的哈希函数组成。二进制位数组初始值全部为0，当给定一个待查询的元素时，这个元素会被一系列哈希函数计算映射出一系列的值，所有的值在位数组的偏移量处置为1

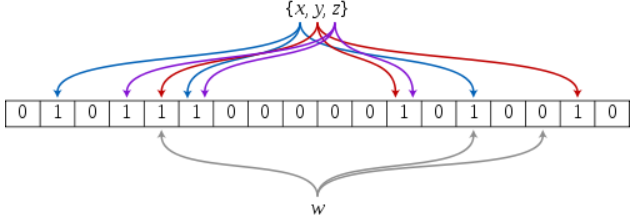
（2）判断元素是否在集合中的方法：元素经过一系列哈希函数计算后得到所有的偏移位置，若这些位置全都为1，则判断这个元素在这个集合中，若有一个不为1，则判断这个元素不在这个集合中

（3）优点：节省空间，采用位数组，2的32次方=4294967296 可以看到42亿长度的位数组占用4294967296/8/1024/1024=512MB 只需占用512MB的内存空间

（4）缺点：有一定的误判，有可能把不在这个集合中的误判为在这个集合中，因为另一个元素经过哈希后各个位置也可能为1

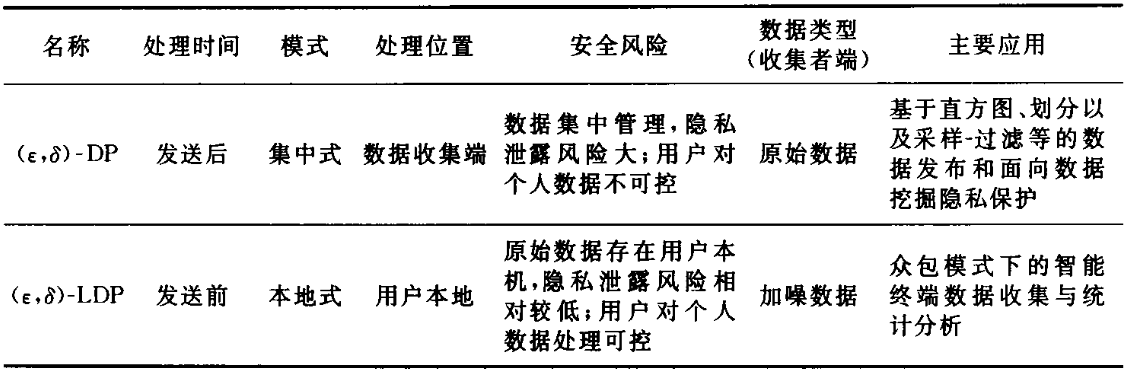
7.差分隐私分类

根据其应用场景及针对数据处理和收集方式的不同，主要存在两种数据分布模型：

（1）集中式模型（分为交互式和非交互式框架），又称为可信管理者模型（Trusted Curator）：服务器端直接存储未处理的原始用户隐私数据，并经过隐私处理等方式后统一对外发布

（2）本地模型（Local Model）：服务器端只能收到用户加噪的数据；用户在向数据收集者发送个人数据前，先在本地加入满足差分隐私的噪声扰动，最后数据收集者根据收集到的噪声数据，从统计学的角度近似估计出用户群体的统计特性，而不是针对具体用户个体进行统计特性推断

8.中位数机制（目前没弄懂）

9.本地差分隐私保护主要思想

（1）不能收集或拥有任何个人的精确信息

（2）可以推断出用户群体的泛化统计信息

10.DP与LDP的区别

两者最重要的区别在于加入噪声扰动的时机不同

11.本地模型下的数据分析流程

每个本地用户用随机器Q扰乱个人数据v得到Z，数据收集者将其汇总得到S，最后进行数据分析；

拉普拉斯机制经常被用于本地模型中，常用于对数值型结果的隐私保护

12.随机响应RR（Randomized Response）

（1）应用：保护敏感话题调查参与者隐私，目前主流的本地差分隐私保护都是基于RR

（2）具体应用场景：每个人不是属于组A就是组B，问题是在不能确定具体个人属于哪组的前提下，估计组A中人数的比例

（3）RR的解决方案：随机选取n个人，随机设备 (可以是抛硬币、摸球模型)以概率P指向A，以概率(1 一p)指向B。在每轮调查中，受访者只需回答设备指向(调查者未知)的组别是否与其真正的组别一致(Yes或No)，这样便可以得到组A人数的最大似然估计

（4）随机响应的效果：实现了ε-LDP，其中ε=ln(p/(1-p))

（5）存在问题：现有的基于RR技术的LDP机制在数据挖掘中具有一定的局限性，只适用于用户数据类型为数值型或范围型， 而数据收集者的数据挖掘任务局限于基本统计，如计数或求中位值等

（6）RR技术及其改进模型在收集群体层面的统计数据而不泄露个体数据方面具有优越性能，目前已成为新的研究热点

13.随机响应RR举例

（1）问题：假设有n个用户，其中艾滋病患者的比例为π，我们希望对π进行统计。于是对目标用户发起问卷调查：“你是否为艾滋病患者？”显然，如果直接获得用户的相应数据进行统计，一旦数据泄露，那么用户隐私随即泄露。因此，我们假设存在一枚非均匀的硬币，其正面向上的概率为p，反面向上的概率为1-p。抛出该硬币，若正面向上，则回答真实答案，反面向上，则回答相反的答案。

（2）推导过程：

1. （step 1）

   理论上，Pr[Xi=“是”]=πp+(1-π)(1-p)，Pr[Xi=“否”]=(1-π)p+π(1-p)。直觉上，当n足够大时，设回答“是”的人数为n1，回答“否”的人数为n2。Pr[Xi=“是”]=n1/n，Pr[Xi=“否”]=n2/n。求解下面的二次方程即可获得π的值

   

   但是，上述的结果并非真实比例的无偏估计，我们用极大似然估计(Max Likehood Estimation)对统计结果进行校正

2. （step 2）

   首先构建最大似然函数：

   

   对数似然函数为：

   

   令

   

   求解可得π的极大似然估计：

   

   由此可得患有HIV的总人数为：

   

14.LDP研究方向

（1）基于随机应答与Bloom Filter的编解码方式研究（RAPPOR）

（2）针对流式频繁项集挖掘Heavy Hitters挖掘

（3）针对智能终端的收集与机器学习

1RAPPOR算法（Google Chrome）

RAPPOR应答被定义为比特位字符串，每一 位都是对应用户端特性报告的逻辑谓词随机应答， 用来收集用户群体的数值和序数值的统计，可以提供ln(3)的差分隐私保护（因为是基于随机响应技术，根据13.随机响应RR可求得隐私预算）

输入：用户数据X，参数k(串长度)，h(Hash个数)，概率参数f、p、q
输出：数据报告s
算法流程：
(1)信号处理。用BloomFilter中的h个哈希函数将X编码成长度为k的01串B。 
(2)永久随机响应(PRR)。利用随机应答技术对B进行扰动得到永久随机响应B'。 
(3)即时随机响应(IRR)。利用随机应答技术对B'进行二次扰动得到即时随机响应s。 
(4)报文。把收集的报告s发送到服务器

RAPPOR在解码过程中结合成熟的假设检验、最小二乘求解和LASSO回归实现针对字符串抽样群体频率的高可用解码框架

存在问题：

（1）使用RAPPOR的数据收集者只能孤立地了解单一变量的分布。实际上，研究多个变量之间的关联更有意义

（2）数据收集者必须事先知道潜在字符串字典、安装软件的报告、名称、hash值，然而这些是不可能作为先验知识的